After a combination of trial and error, reading the Blender Python API, reading Blender dev web pages and further research on the Internet I was able to recreate Blender's skinning algorithm using a Python script. The advantage of using Blender's python scripting was that I could run my script and compare its results with Blender's native pose deformation system.
In pseudocode, the skinning algorithm is:
Deriving the Inverse Pose Transform
Step 1: Recreating Blender's armature posing algorithm using a python script
Step 2: Converting the per vertex skinning algorithm to a mathematical function
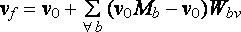
Step 3: Finding the inverse skinning function g such that v0 = g(vf) .
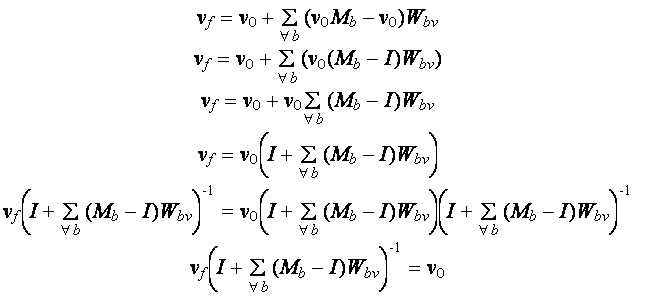
Step 4: Converting the mathematical solution to an algorithm
Envelopes Must be Frozen for the PSD to Work
For each vertex v of a mesh:
originalv = Vector(v) // save a (deep) copy of v
For each bone b:
delta = originalv * b.localMatrix - originalv
v = v + delta *normalizedWeightOfBone_b_forVertex_v
Each vertex goes through the following transformation:
For each bone b: delta = originalv * b.localMatrix - originalv v = v + delta *normalizedWeightOfBone_b_forVertex_v
By substituting for delta, this can be rewritten:
For each bone b: v = v + (originalv * b.localMatrix - originalv)*normalizedWeightOfBone_b_forVertex_v
Replacing the for loop with a summation over all bones b we get the final vertex coordinates in terms of the initial vertex coordinates (upside down 'A' is the 'for all' symbol):
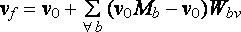
Where:
vf is the final skinned vertex
v0 is the vertex prior to skinning
Mb is b.localMatrix
Wbv is the normalized vertex weight of bone b for v0 and vf .
Note that we have now expressed vf as a function f of v0, in other words we have vf = f(vo) .
vf is the final skinned vertex
v0 is the vertex prior to skinning
Mb is b.localMatrix
Wbv is the normalized vertex weight of bone b for v0 and vf .
Note that we have now expressed vf as a function f of v0, in other words we have vf = f(vo) .
Step 3: Finding the inverse skinning function g such that v0 = g(vf) .
Below is a step by step solution (note that I is the identity matrix):
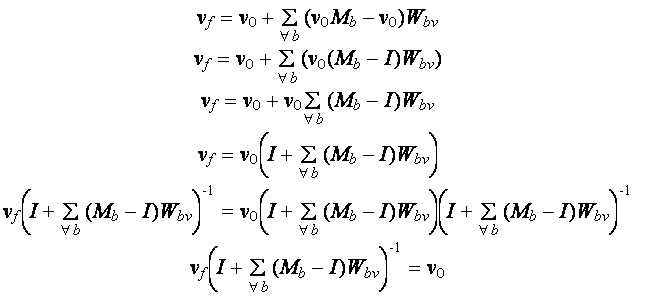
We have now ended up with a formula expressing v0 in terms of vf . This is g(vf) .
Step 4: Converting the mathematical solution to an algorithm
By examining g(vf), we can work from the inside of the mathematical expression outwards to build the code. At the beginning of an interation of the outer loop (over the vertices) we start with vf. At the end of the interation vf is overwritten with v0. Here is the final inverse transform pseudocode:
For each vertex v of a mesh:
sigma = Matrix filled with zeros //the accumulator
for each bone b:
sigma = sigma + (b.localMatrix - I) * normalizedWeightOfBone_b_forVertex_v
v = v * invert(I + sigma)
In Blender, when the envelope option is active for a certain bone, an algorithm dynamically determines the amount of influence exerted by the bone on vertices using bone envelope sizes and its proximity to the vertices. After calculating the inverse transform the unposed shape's vertices are in different locations and therefore now have different bone influences and therefore different weights. Bone weights must be constant for the inverse transform to be calculated, otherwise by the end of the calculation, the starting conditions are no longer the same and the solution is invalid. I believe that finding the inverse pose transform when (dynamic) envelopes are active is impossible unless the envelopes are made permanent by baking them into weights or making envelopes only apply to the basis shape. A similar situation to the above exists in Lightwave and may be responsible for problems users have encountered when setting up smart-skinning for vertices influenced in part or in full by bone envelopes.
